

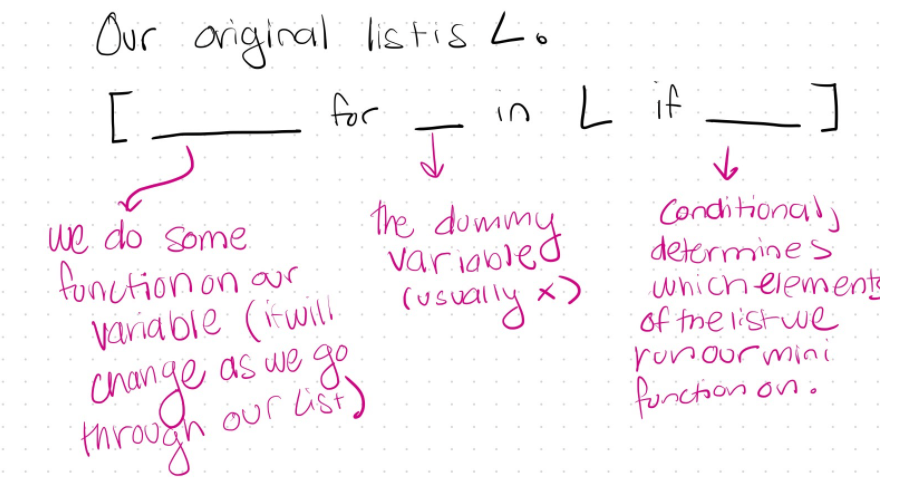
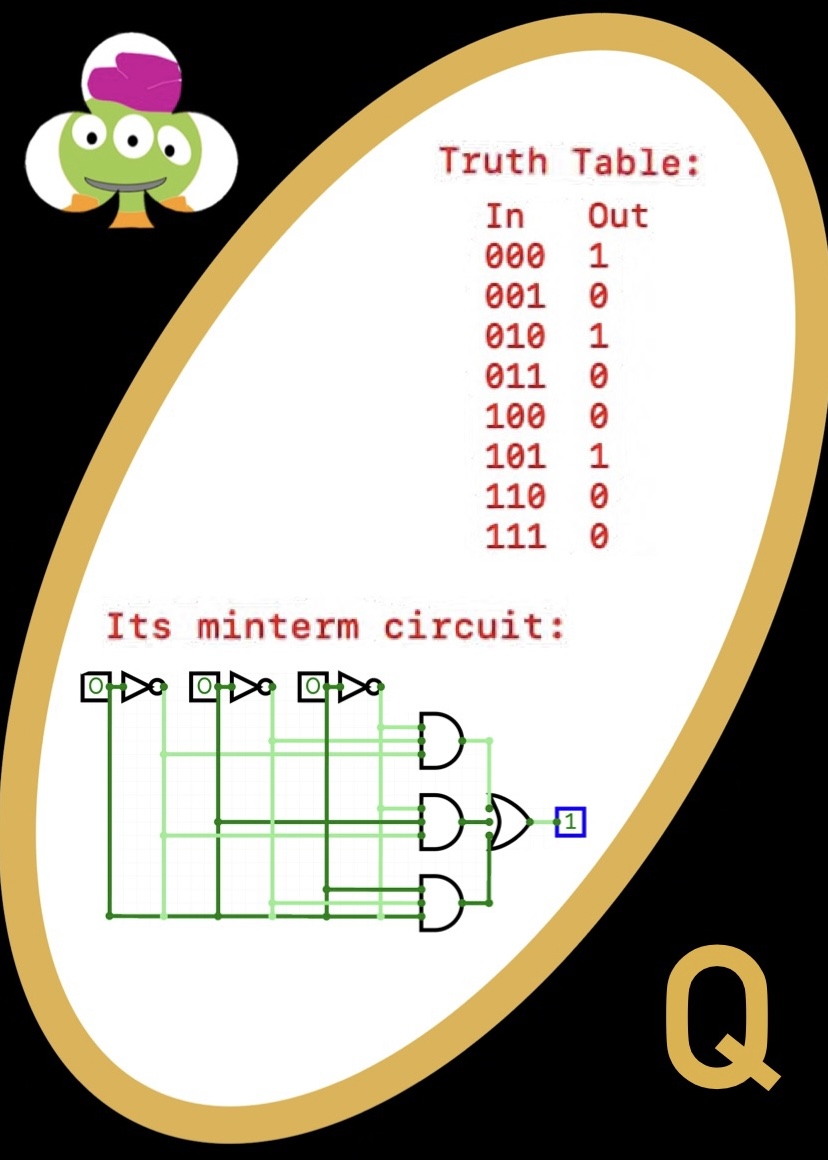
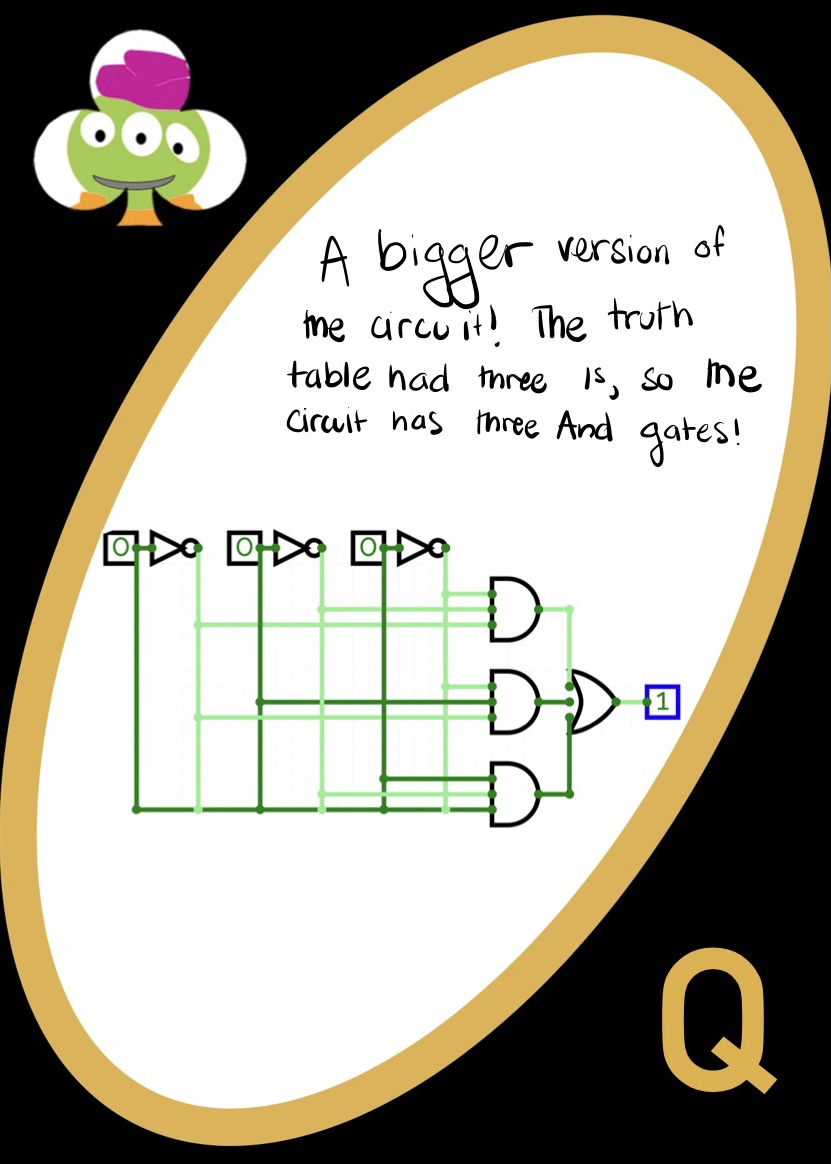
Minterm Expansion Principle
Given a boolean function — represented as a truth table — how can we construct a machine that computes that function? The answer is combinational logic — a technique for using gates to implement boolean functions. A minterm is an AND gate that is connected to all its inputs directly or through a NOT gate. Minterm expansion (sometimes called the “minterm expansion principle”) is an algorithm for transforming a truth table into a circuit:
- Look at all possible combinations of values for the inputs to the function: For each combination of values that should cause the function to output 1, build a minterm that outputs 1 only for those input values (and 0 for all other input values)
- OR all the minterms together
Click here for more info


Image Compression
Take a closer look at the bottom of the pop tarts box. Can you read the text? I certainly can’t! This is because the image has been compressed: a few times, actually. As part of CS5, everyone gets to code an image compression algorithm. To do this, we need to think about any image we’re given as a string of binary digits, like this one: ‘01000010110101001010101’
To compress an image, we literally compress the binary string representation of the image. For our algorithm, we have a few steps to think through.
- We need to think about our string as a way to carry simple information. In this way, we are going to re-write that information. Strings with lots of repetition should be easy to condense. We can write those repeated strings as a product of two things. (Hint: consider multiplying the character we are repeating by … something … )
- Once you’ve figured out how to write a repeated number as a product, we can make it regular. We can decide how many times is the most that we can repeat a number - writing this in binary, of course. All the other numbers we’ll need to “pad” with front zeros
- Write the code! We are going to iterate through an entire binary string recursively, and decide how to express certain repeated values as one string that is (hopefully) shorter. Consider writing helper functions that: count the number of repeated 1’s/0’s, convert base 10 integer counts to binary counts.
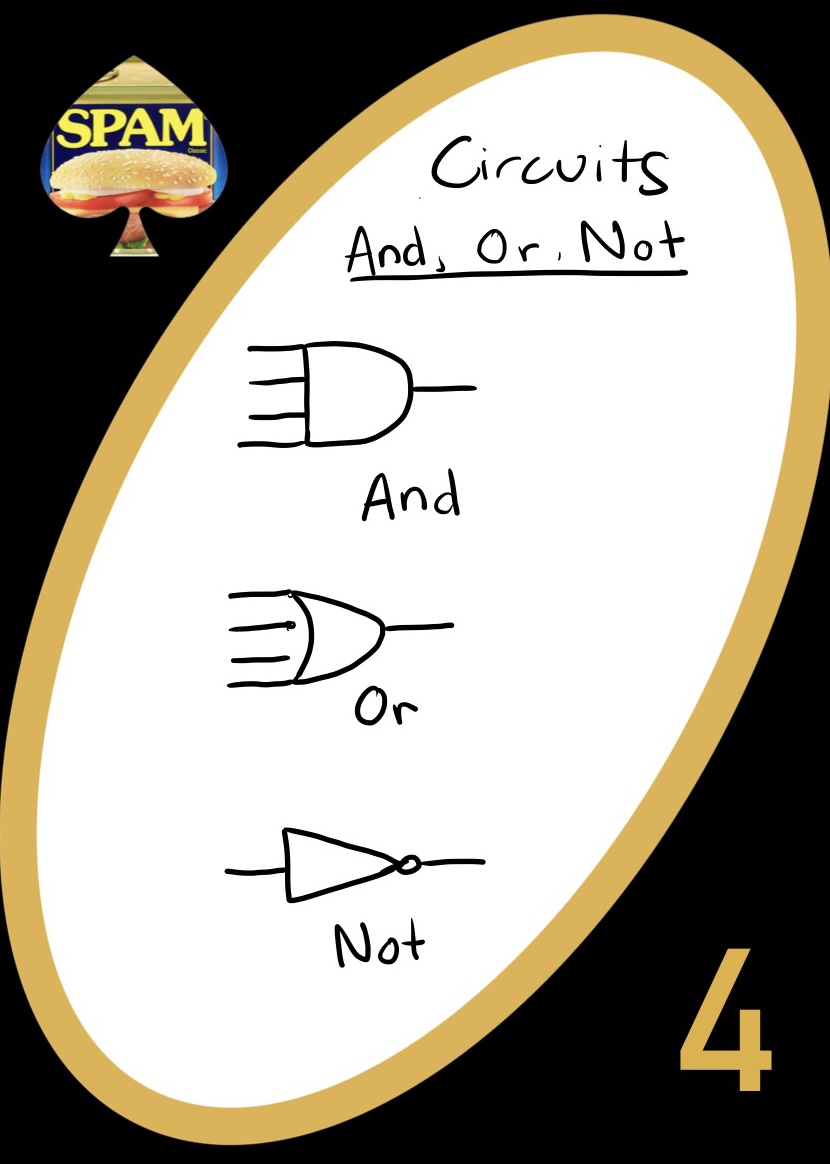
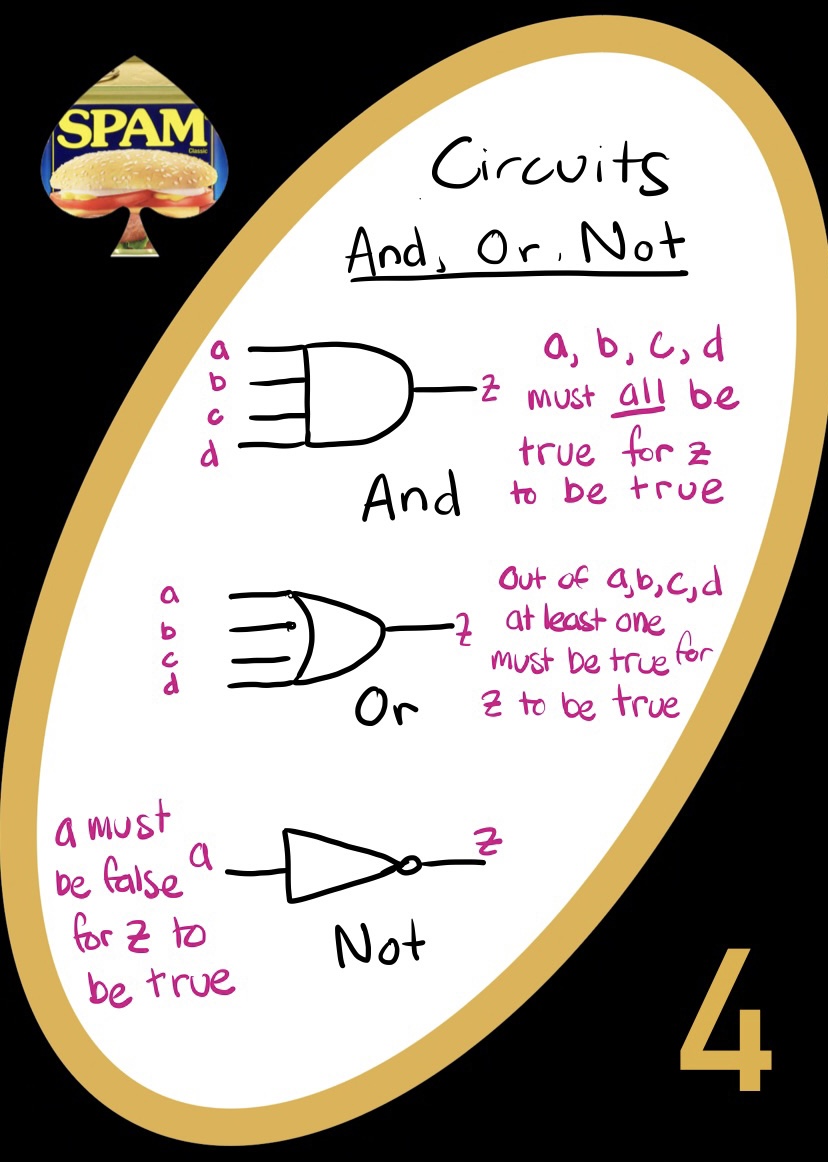
Circuits
Use the circuits site!
There are several important gates that are used in logic circuits
- AND gates output True if all inputs are True. Otherwise they output False
- OR gates output True if at least one of the inputs are True. Otherwise they output False
- NOT gates simply reverse the input! Inputting True outputs False, and inputting False outputs True


Binary to Base-10
In python, there are built-in functions to convert between binary and base-10. For example, bin(42) will return the string "0b101010" (the "0b" is python's way of marking a binary number). The int() function can convert from an arbitrary base to base-10 by passing in a second argument. For example, int("101010", 2) parses the string as a binary number and returns 42
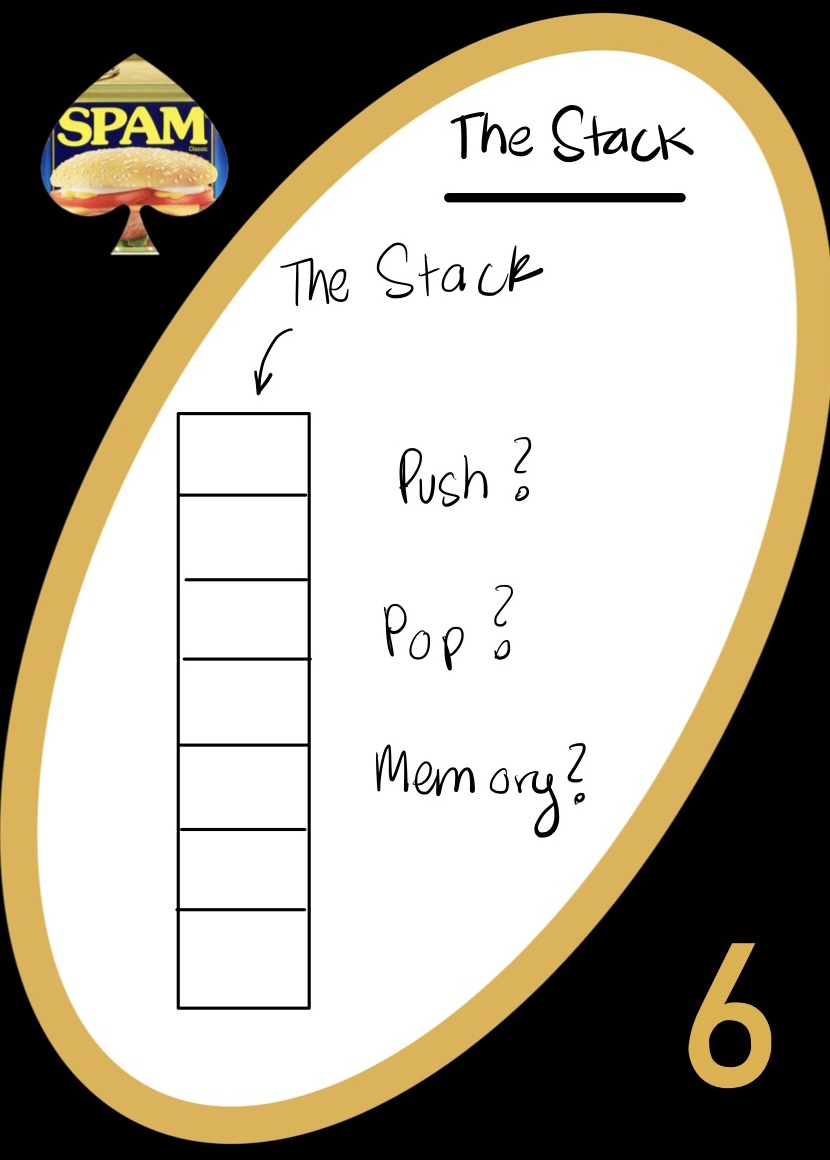
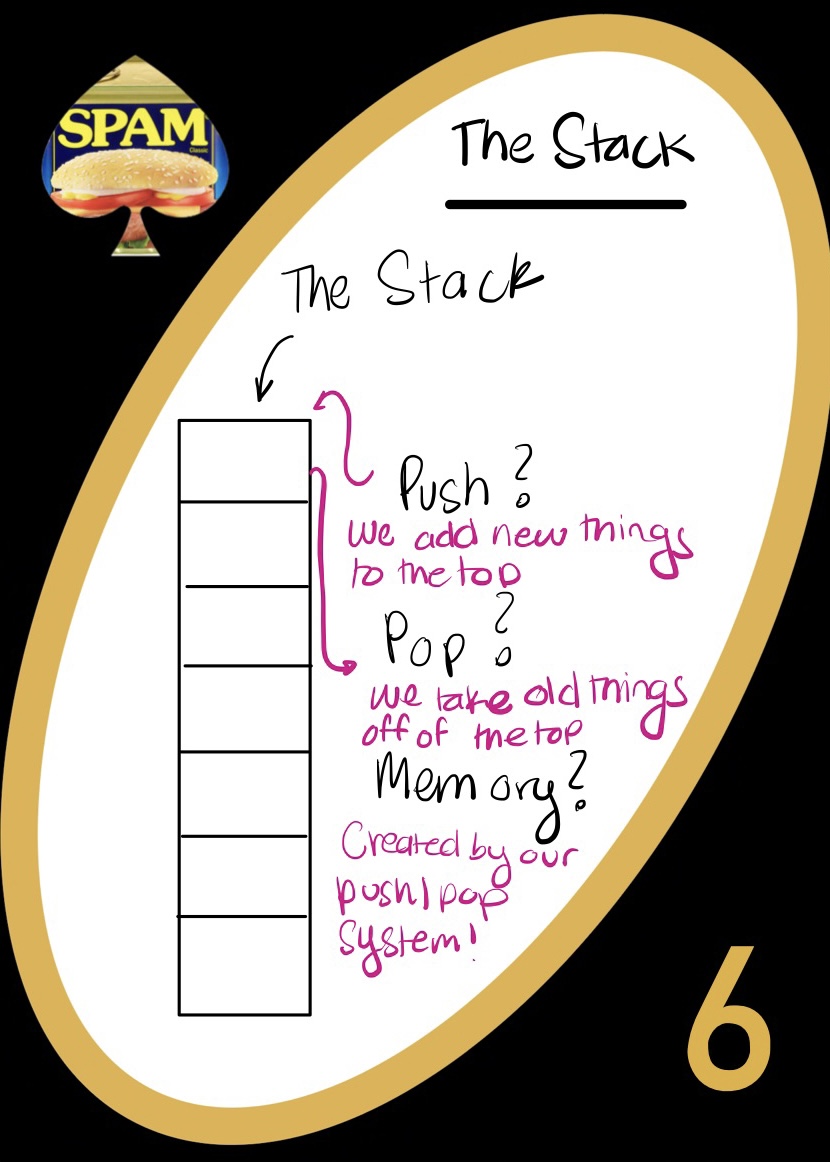
The Stack
The stack is where all of our stuff gets stored! This is where we get computer memory from - stack pointers let us traverse (almost literal) stacks of information. We put “elements” or information into the stack, and it changes size when we do. There are two main methods that we need to consider when learning about the stack:
-
Push means we are putting a new element onto the top of the stack
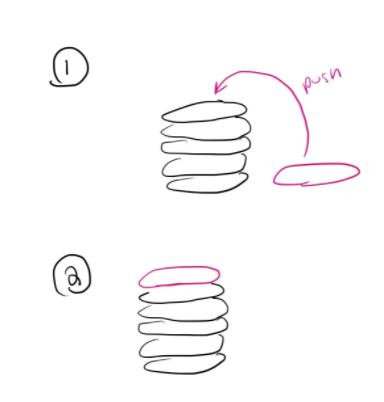
-
Pop means we are taking an element from the stack
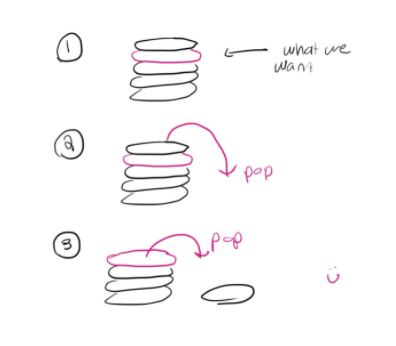
Pushing/popping happens around the element on top of the stack. We can only access from the front/top! If you want more practice, try using the stack at our website:
HMMM with Wally!
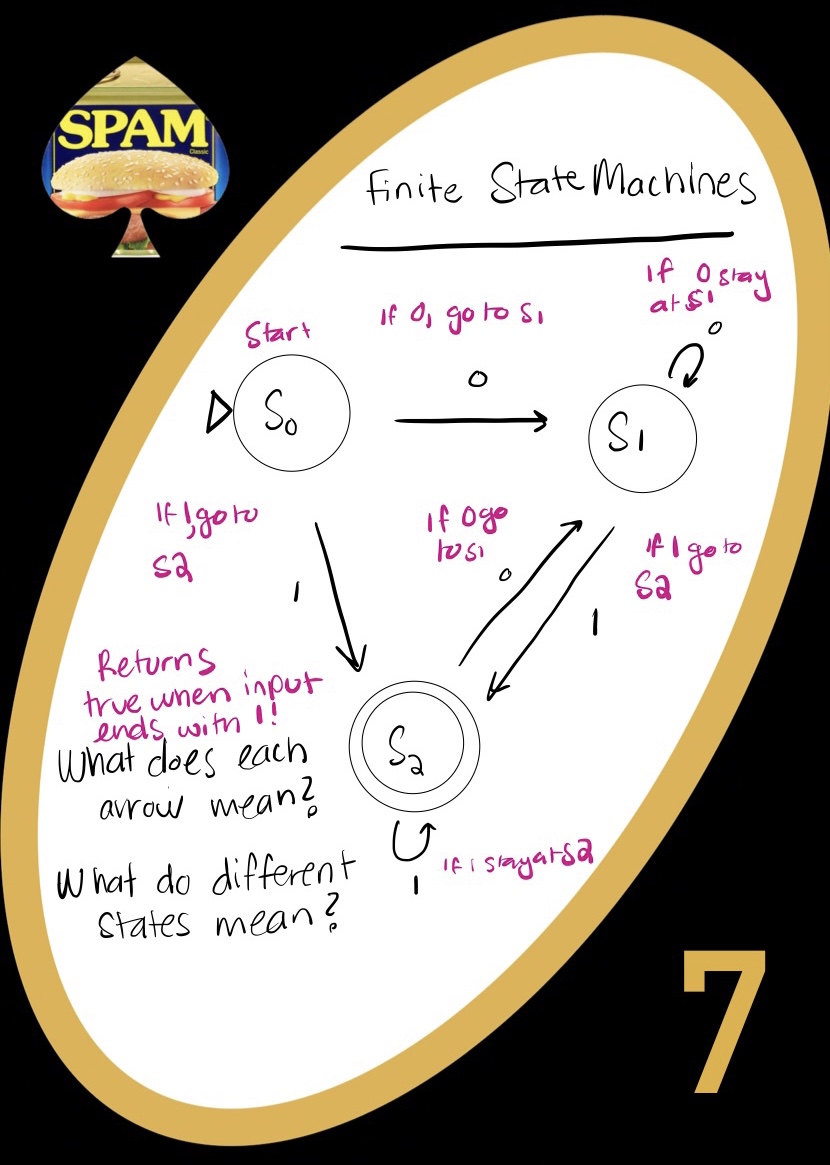
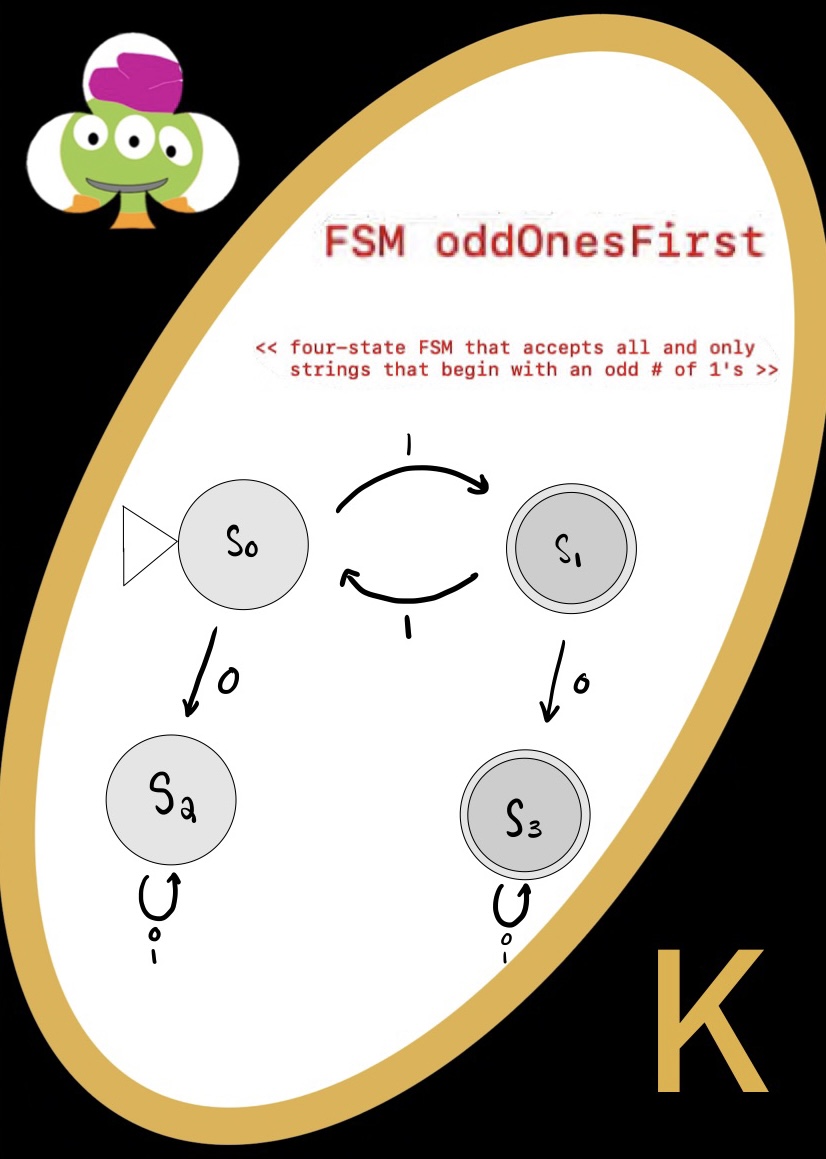
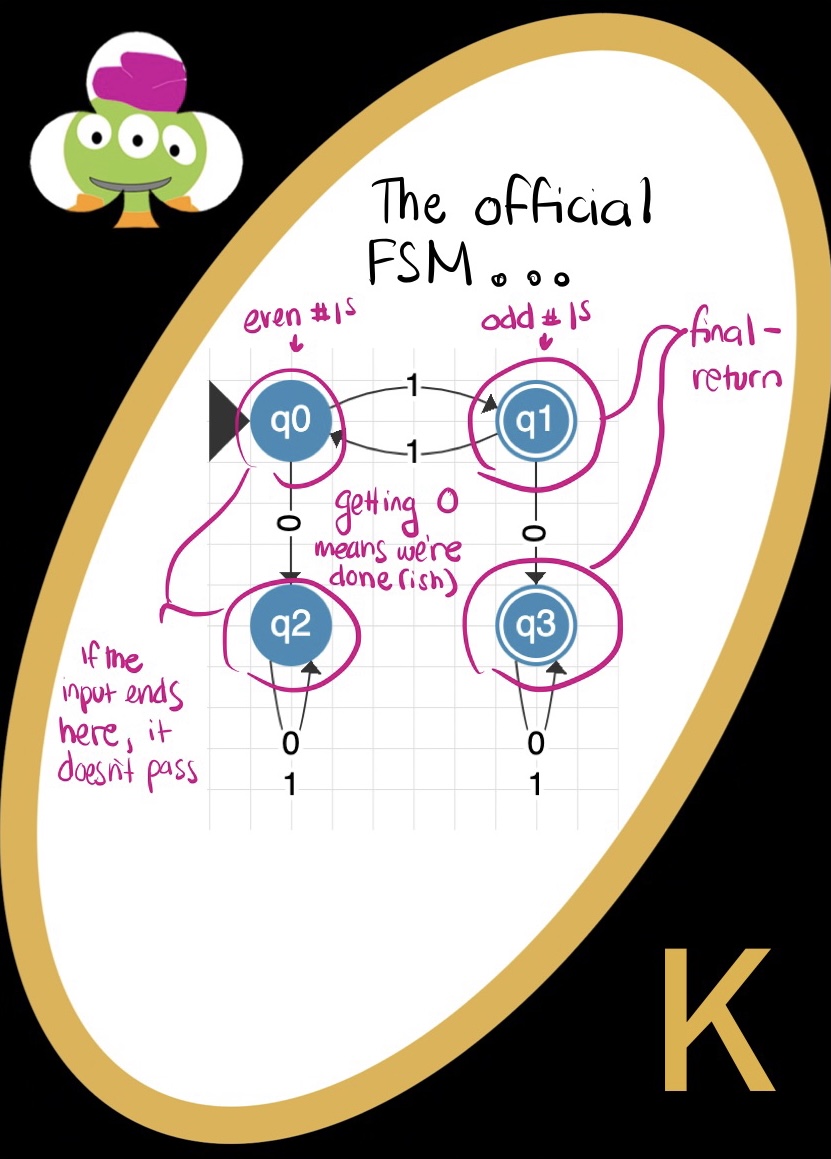
Finite State Machines
A state is a situation of the ‘system’. I can have a light switch that is on or off, then there are 2 states. We represent these states with circles in our FSMs. A state can either lead to a 0 or a 1 (for us). Either that state happens and triggers one thing, or that state happens and triggers another thing.
- You can stay in the same state
- You can move to a new state

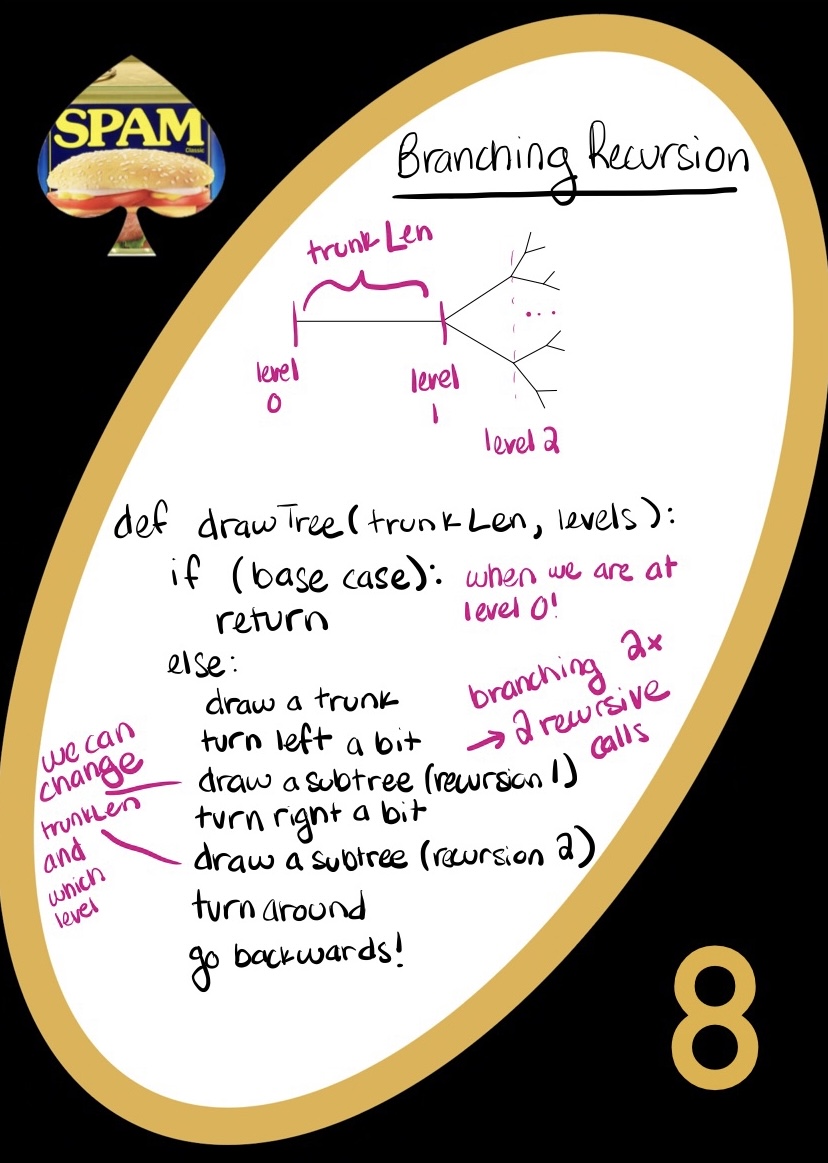
Branching Recursion
Branching recursion is just like normal recursion, except that different cases end up with different recursive calls. It can help to picture a recursion ‘tree’ - each different recursive call makes its own branch. This is different from normal recursion in that you need to check two different recursive calls to get the job done.
The example on the card draws a recursive tree - it branches twice each level, just like our recursion! On the pseudocode, you can see that the subtrees (left and right) are happening simultaneously, and each represents a different path to get to the base case. The power of the recursion here is that our computers can make this tree, see the best choice out of all the choices (when we care about outcomes), and come back to the start of the tree without breaking a sweat.
We might want to use branching recursion when there are two distinct paths to take in a problem. Besides trees, some examples include exact change, scrabble outcomes, or even the most recent common ancestor in biology. The thing that all these seemingly different problems have in common is that they ask for a specific result, and there are two different outcomes at each choice. We can look closer at exact change: if we want to make a total from a pile of coins, we are always either using or losing a coin. Useit or Loseit are then each their own outcomes: we can recurse through both for every single coin until we get a set of combinations that gets exact change for a total!


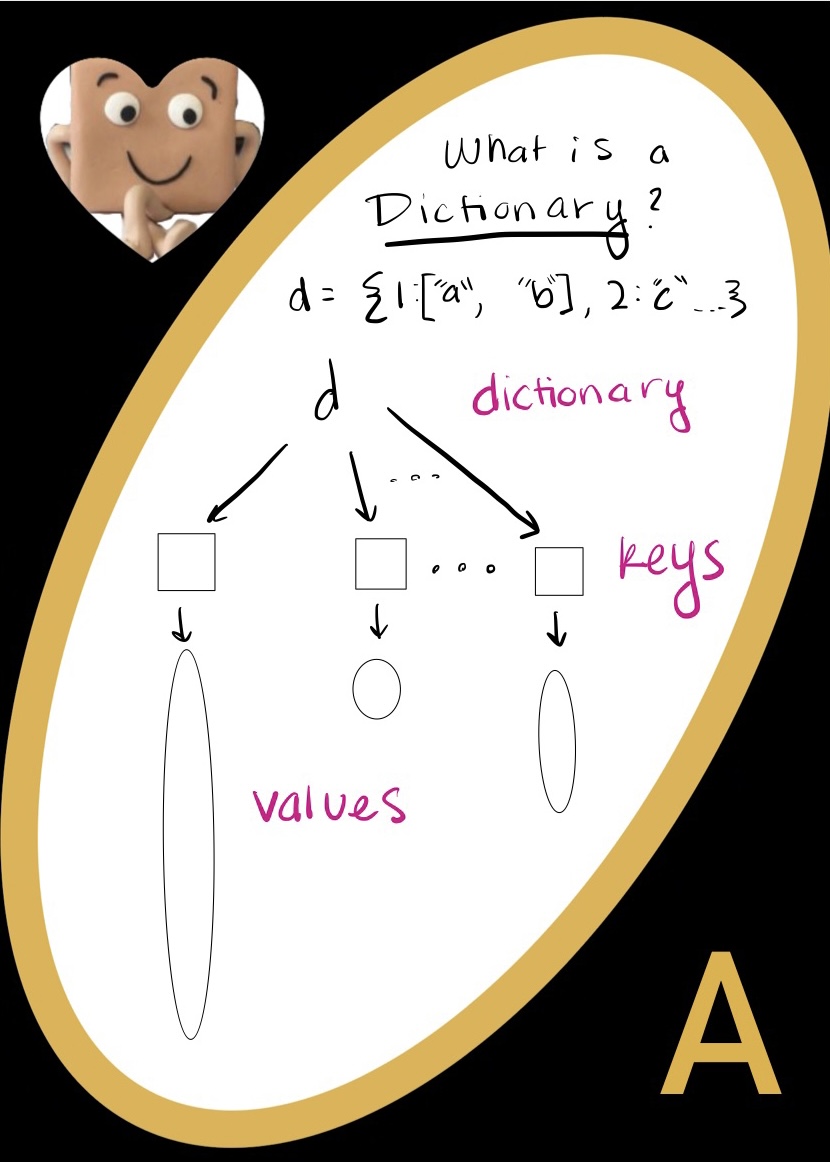
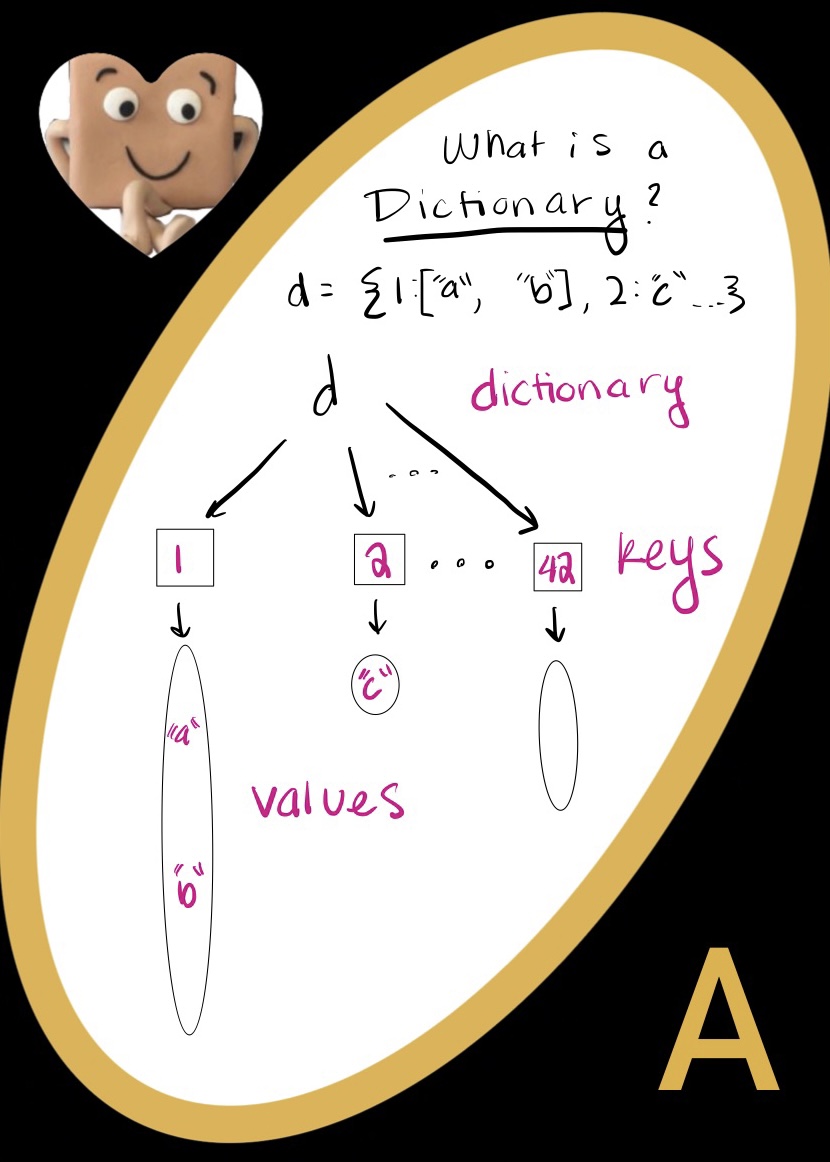
Classes vs. Objects
Classes and objects are similar (which is sometimes confusing). However, classes are different from objects.
- Classes are ‘cookie cutter’ that lets you make many objects of the same type. Those objects should all have things in common, since they’re specified by the class!
- For example, I can have an Alien class that makes three eyed aliens, klingons, and daleks. Classes are like object making factories!
- Objects are the real things that have attributes that you specify with a class in order to make the object
- If our class is Alien, the alien that you make with that class is an object! I can make a three eyed alien named burt who is an object that belongs to the Alien class. I can also make him a klingon friend named
 (or in English, chad) who will be an object that belongs to the Alien class. Finally, we can make Davros who is a Dalek, and is also an Alien
(or in English, chad) who will be an object that belongs to the Alien class. Finally, we can make Davros who is a Dalek, and is also an Alien - When we make objects from a class, we are saying that they have attributes that we specify with the class


Example: Classes and Objects
Let’s write an example Alien class that makes a 3 eyed alien object. First, we can note what we want all aliens (or objects belonging to the Alien class) to be able to do. Aliens should be able to count to 42, have names, and they can have 3 eyes. Since these are all things that every alien can do / have, we can write them in our class.
In our example, each time we make a new alien, we need to specify the Alien attributes in the constructor. To our constructor, we can send the number of eyes our Alien will have, and their name. Then, when our Alien gets “made”, it will have the attributes we specify! Next, we need to write the repr function. This function represents our Alien of choice as a string! This one is left to your imagination.
Onto methods! The next thing we need to do is say what our Aliens can do. Here, we can write a method (which is just a fancy word for function) that specifies how our Alien can count to 42! Aliens will need to do other things of course, but for now, let’s make a sample alien. We get to make a 3 eyed alien. This Alien is stored in the variable instance aliiien, and we use the class Alien, specifying aliiien’s name (“aliiien”) and how many eyes aliiien will have. All Aliens can count to 42, so we don’t need to say whether aliiien can count to 42.
That’s it! You’ve made an Alien!


What's in a Class?!
All classes have a constructor, a repr function, and maybe some methods.
- Constructor
- This is where you actually make the object - self! Self is different based on what object you are making. The class treats self as the same
- May need to specify what attributes every object will have (ie, do all aliens have eyes, etc)
- You always need to write
__init__(self, *kwargs) - Inside, you specify how the variables you pass in get assigned to the object
- Repr
- This function returns a representation of the object that we can see (as a string)
- This should return different things based on what you need your object to do
- You will always write
___repr__(self) - Methods
- Methods are just functions that all objects of a class can do. Maybe all aliens can eat spam. Then we would write a method eatSpam(self) that says how aliens eat spam.
- When we call methods outside the class, we need to know what object is doing the method and all the variables we pass into the method (besides self, since self is the object)
- We do this by saying
object.method(variables). Look familiar?

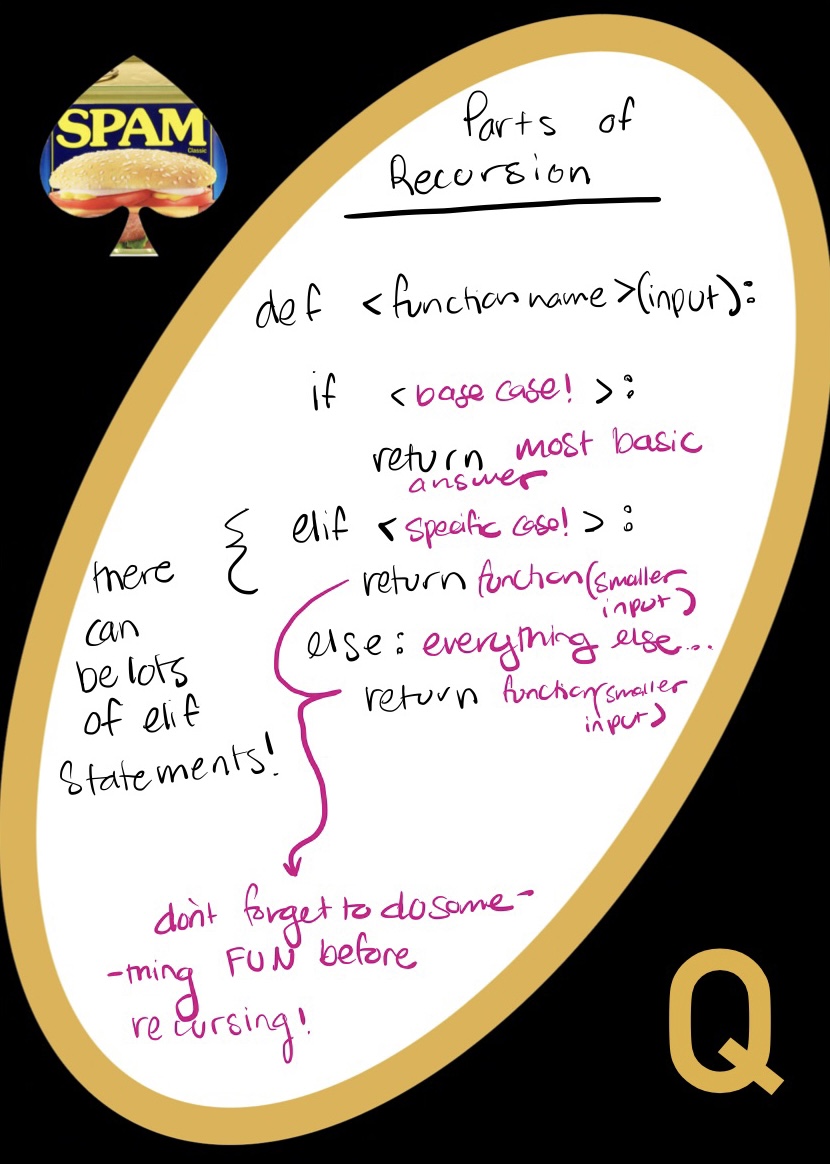
Parts of Recursion
Recursion always has at least two parts, and it usually has three!
- Base Case
- The base case tells us when to stop
- When we get to the end of our input what should we return? Sometimes you will be inputting a string and want an integer (say, if you wanted to count the i’s in aliiiiiiiiien) so we’d check whether a string is empty and return a number, in this case, 0
- Recursive Part
- We can think of the recursive part as the actual stuff we want to do to our slice of our input. Sometimes this is broken into multiple steps; you always handle the specific case first, and then everything else
- For example, if we wanted to count how many i’s there are in alliiiiiiiiiiiien, we would take each letter at a time. We would ask our function: is the first letter an i (specific case)? For every other letter, we just skip it and keep going down the string (the general case)
- In our recursive call, we will always handle one piece of information first, and then let our own function do the rest, with all of this stuck together by some operation glue
- In our count i’s, we take one letter, check if it’s an i or not, and add the result to the function running ON EVERY OTHER LETTER besides the one we have just handled
- If you do this enough times, you get to the end, which is our base case!


For vs. While Loops
For loops and while loops are pretty similar! In fact, you can write every single while loop as a for loop.
forloop- We want to use a for loop when we know where our testing is going to end.
- If we wanted to go through an entire list counting how many 42’s we have, we know exactly how long the list is. So we can say, "for every element in the list, do this thing"
whileloop- While loops are for indefinite endings - when we don’t know where in a situation we want to stop
- If we took the same list as before, but asked a different question, we could use a while loop. Let’s ask: How many 1s until we hit a 42? In this case, we don’t know where the first 42 is. We can write, while our list doesn’t have a 42, keep going down the list
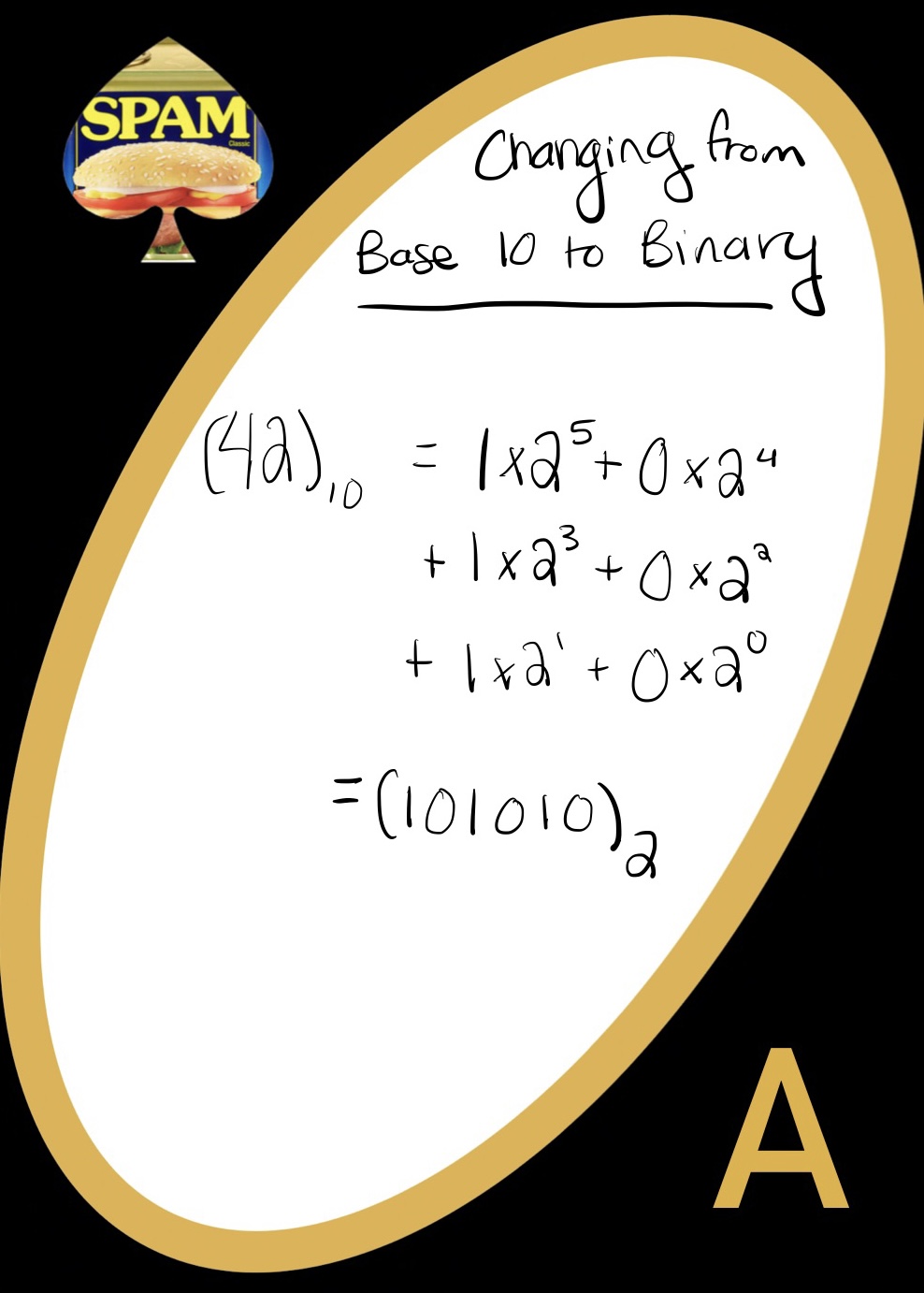

Changing to Binary from Base-10
To get a number into binary, the question we’re really asking is: how many times does 2 go into our number? How about different powers of 2? We can answer this by dividing by different powers of 2. If we start by dividing the number by 2, we can count how many times \(2^0\) is in that number (it will always be either 0 or 1). If we divide by 2 again, we are counting how many times \(2^1\) is in that number. Let’s write out this process:
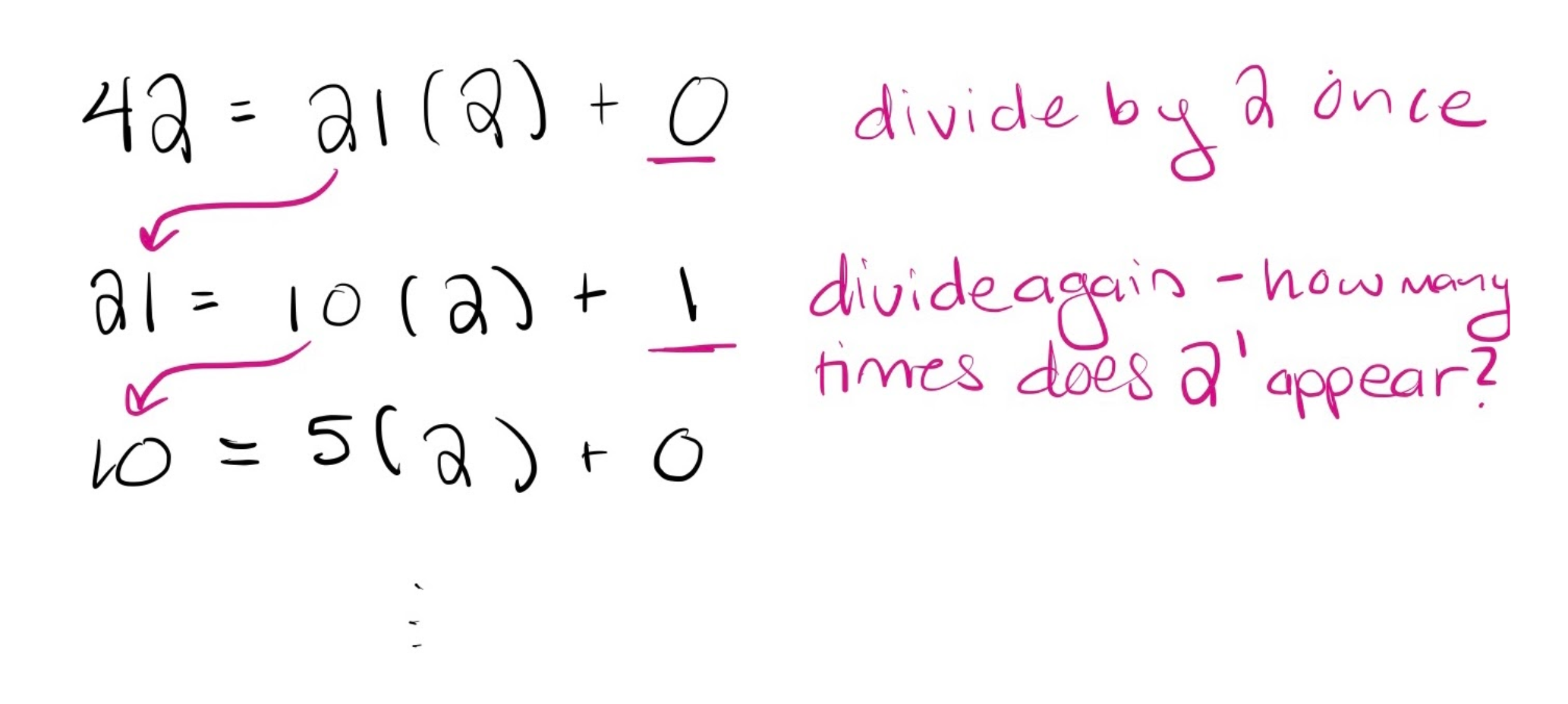
We’ve BASE-ically just written out which power of 2 we multiply by a remainder! This is our number in base 2. If you want to apply this to code, consider recursion. Every time we divide by 2, we are making our number smaller and smaller. We are keeping track of what is left in that division. If we do this until the number gets to be 0, we have reached a base case. We can then add up those digits and - voila! You have a lovely base 2 string of 0’s and 1’s.




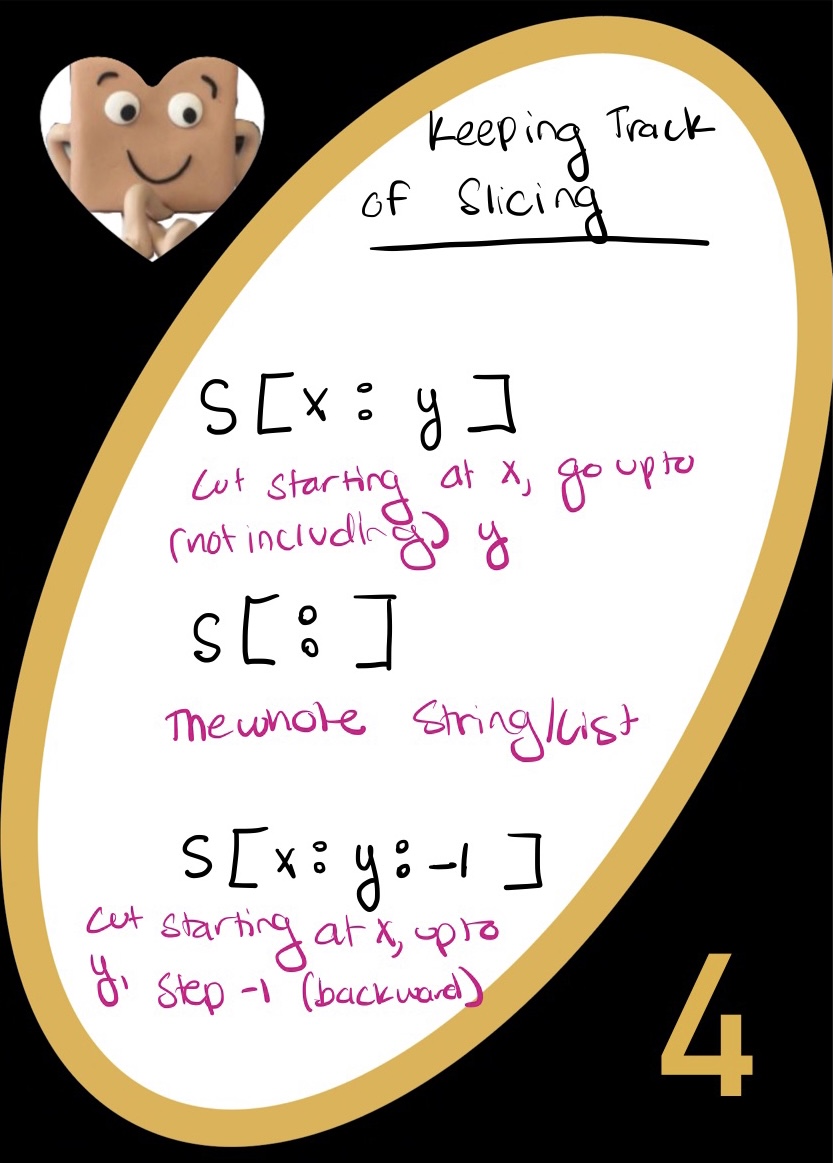













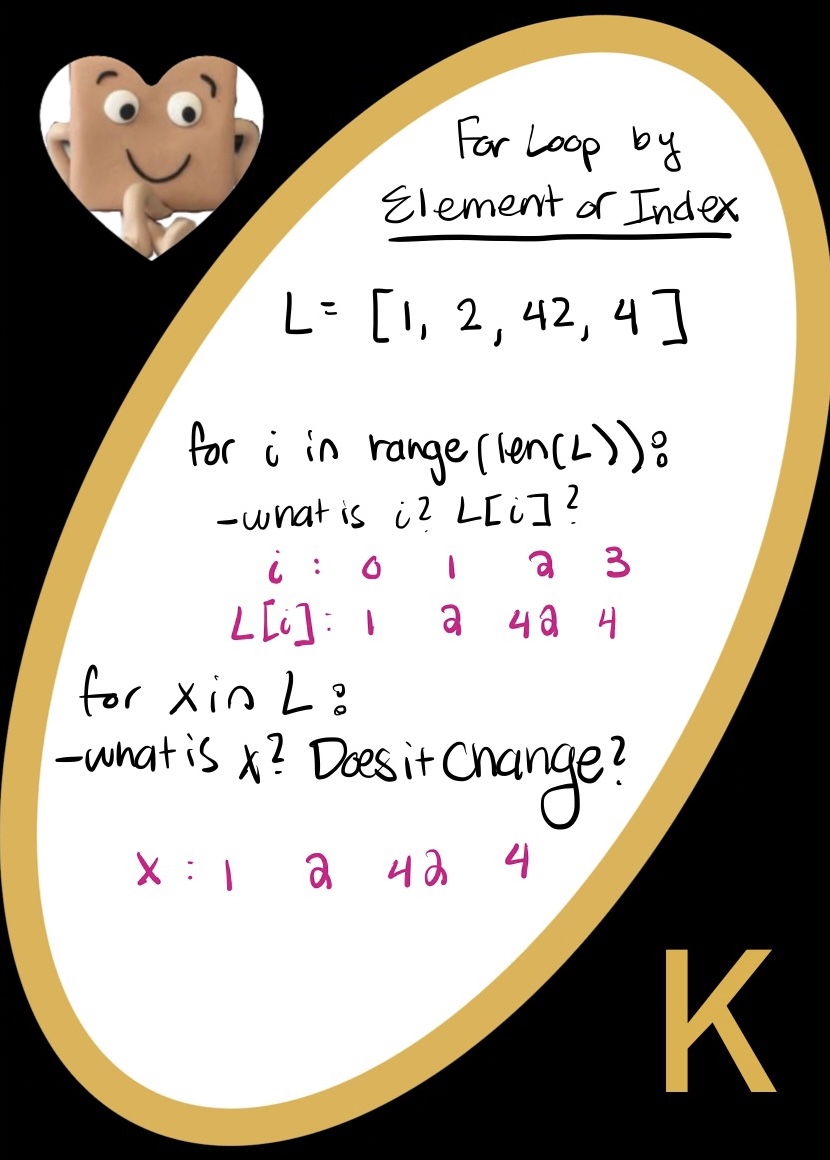
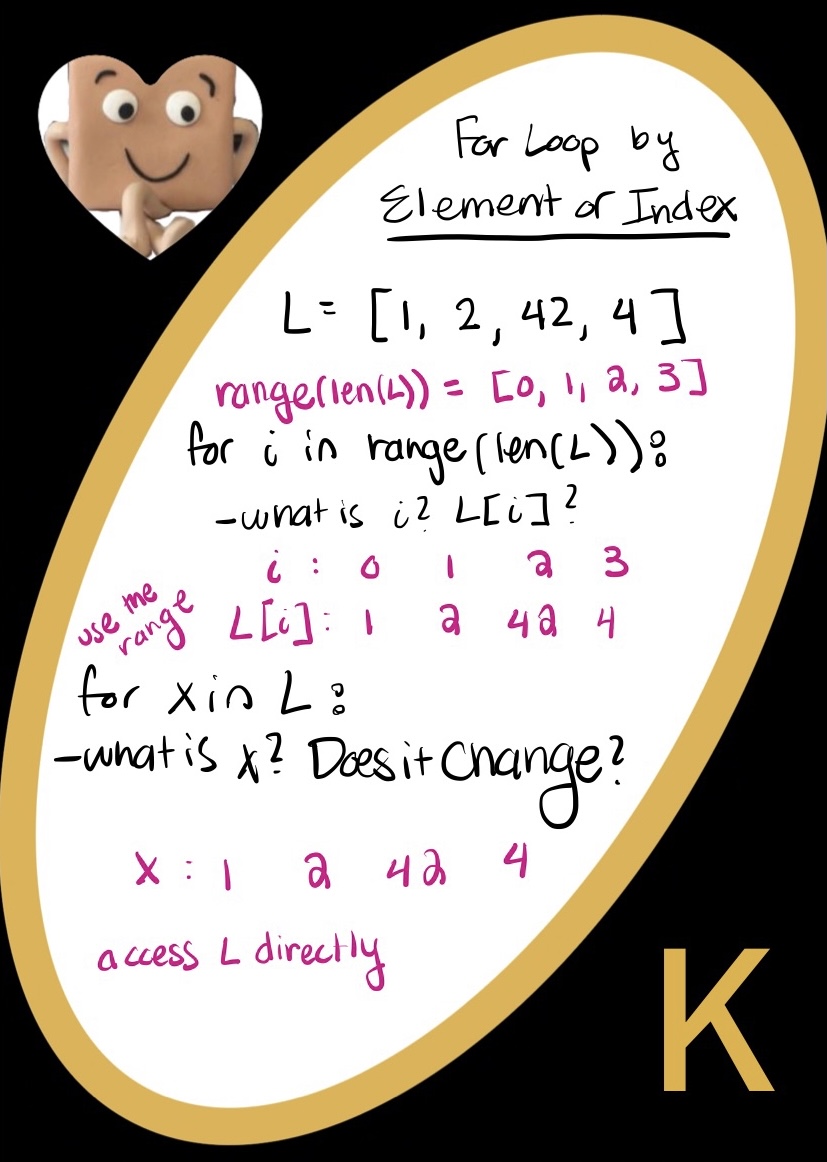











































 Where the black represents the numbers in the set as points in the complex plane. Keep zooming and there will be more numbers in the set, forever!
Where the black represents the numbers in the set as points in the complex plane. Keep zooming and there will be more numbers in the set, forever!

